Best Of 30POV: Quantum Bananas & Cherry Pi

“Best Combination of Popular Culture with Quantum Nerdiness”

Quantum Bananas and Cherry Pi.*

I’m obsessed with the notion that two things never touch.

I don’t know where I read it or heard it or saw it first—this crazy idea involving quantum mechanics andelectric fields and chemical synapses and Zen mysteries—but it’s something to ponder: that no matter what we think we feel, there is, on an invisible atomic level, a space between everything.

Let’s back up.

There’s a silly romantic comedy with Tim Robbins, Meg Ryan, and Walter Matthau as Albert Einstein, calledI.Q, which illustrates ideas on infinity, space, and relativity in a cute if not cheesy way.  Meg Ryan and Tim Robbins are at opposite ends of a dance floor.  Meg asks Tim if he’s familiar with Zeno’s Paradox, whereby to get from Point A to Point B, we must cross the halfway point between them.  Once reaching that halfway point, there is a new halfway point between them.  Then, at that halfway point, there is another.

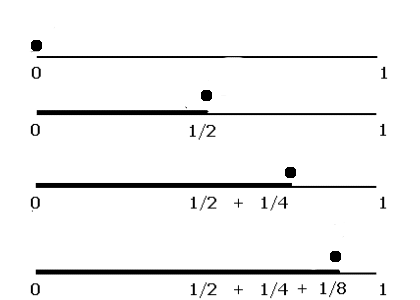
This is where Paradox creeps in spookily: to get to one’s destination, you have to cross the halfway mark between yourself and wherever you’re going, but between Point A and Point B, there are an infinite number of halfway points, and if you stopped at each one, you’d never reach your destination.  Of course, Robbins goes halfway toward the girl.  Ryan goes halfway to the boy.  They go the next two or three halfway points, flirting.  They eventually meet at the middle of the dance floor, embrace, and one says “So how did that happen?”

Zeno’s Paradox stems largely from Aristotle, who said, That which is in locomotion must arrive at the half-way stage before it arrives at the goal, which makes logical sense.  But what of those infinite halfway points?  How does anything reach its goal?  How do we know if we ever get to Point B?  Are we ever reaching—and eventually touching—anything or anyone?

I don’t even want to believe in infinity.  I think it’s a vague theoretical, mathematical notion with a really cool symbol:

Ideas like Pi, again, a really cool symbol, entrance and infuriate me.

It goes on forever.  Forever?  What the hell does that mean?  3.141592654ever?  No end?  No repeating?  No pattern?  The longest decimal representation of Pi, according to the handy-if-not-always-dependable Wikipedia, is over five trillion digits.  And counting.  Why?  I feel like if I could answer this question—and no one can, apparently, not even people ten times as smart as me—I’d be able to answer why people fall in and out of love, why earthquakes decimate nations, why kids get cancer.

I like finiteness.  I like exactness.  This spooky math and physics simultaneously explains everything while destroying everything we think we know.

Let’s get really boring:

“In the nervous system, a synapse is a junction that permits a neuron to pass an electrical or chemical signal to another cell.” (Wikipedia, of course).

But look at this picture.

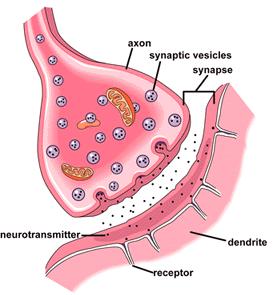
There is a gap.  There is a space.  All the information that transfers pain and pleasure from our body to our brain and back again…transfers in waves and particles through nerve cells that are connected—but not actually touching.

This is a physical metaphor—or rather a microcosm—of the spaces between what we actually touch.  According to quantum mechanics, my fingers and the keys on this keyboard are separated by an infinite world where electric fields are melding, where gravity and motion and direction are making words appear, but where nothing but microscopic particles are banging against each other in the inconceivable space where I perceive the sense of touch.

How we interpret “touch” impacts what we think about all this, of course.  I still think we touch things in the simple sense of the word: I think people can start fires with friction; I think ignitions turn with a key; I think we lift and hold our children; I think we clutch our pens and write; I think kisses lead to more kisses.  But still, I wonder, and I pretty much do believe that there is something separating us, always, from everything and everyone.  Maybe that’s part of the reason we try to get closer to people we love, the need, the desire, to meet in that place where our nerve cells, on invisible fire, mingle and dance without truly meeting.

Look at the Enso.

This circle is very important in Zen Buddhism and can represent strength, enlightenment, and much more.  They’re not always broken circles like the one above, but the idea of a broken circle appeals to me: the circle, a thing with no beginning and no end, but one that isn’t fully connected, imperfect and incomplete, something that looks like it’s trying to reach its destination, and can’t, but still tries, and tries forever.

That seems like the way we are, when we’re at our best.  And it’s the only forever—the only infinity—that makes sense to me.

Ask me about an infinite number of monkeys, sometime.

They wrote this blog once.

But it was more concise.

And then they laughed and swung around the laboratory, never wondering for a minute whether they were touching anything.  They just knew what they knew, and celebrated with bananas.

________________________________________________________

*”Quantum Bananas and Cherry Pi.” Orig. Pub. Date: 12/24/2010. Vol II, Issue 4 ~ Paradox ~ 30POV.com; All rights belong to the original author.